해시테이블
해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 색인(index) 삼아 데이터의 값 (value)을 키와 함께 저장하는 자료구조를 해시테이블(hash table)이라고 합니다.
이 때 데이터 가 저장되는 곳을 버킷(bucket) 또는 슬롯(slot)이라고 합니다.
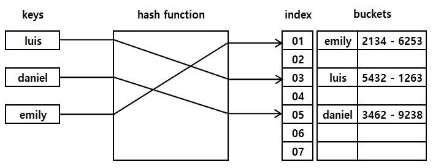
Direct-address table
키의 전체 개수와 동일한 크기의 버킷을 가진 해시테이블을 Direct-address table이라고 합니 다.
Direct-address table의 장점은 키 개수와 해시테이블 크기가 동일하기 때문에 해시충돌 문제가 발생하지 않는다는 겁니다.
하지만 전체 키 중 실제 사용되는 키의 개수가 적을 경우 메모리 효율성이 크게 떨어집니다.
대표적인것이 배열 인덱스를 키로 사용하는 방법입니다.
예) 다음 수열에서 각 숫자의 빈도수를 구하세요.
array = [55236, 55238, 55239, 55240, 55236, 55236, 55238, ....55240]

충돌
해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환하기 때문에 해시함수가 서 로 다른 두 개의 키에 대해 동일한 해시값을 내는 해시충돌(collision)이 발생하게 됩니다.
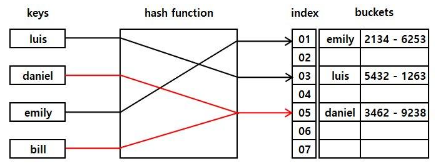
아래 그림은 이름-전화번호를 매핑하기 위한 해시함수를 개념적으로 나타냈습니다.
예시의 해시 함수는 ‘daniel’과 ‘bill’를 모두 ‘05’로 매핑해 해시충돌을 일으키고 있습니다.
충돌해결(체인법 : Separate Chaining)
해시충돌 문제를 해결하기 위한 간단한 아이디어 가운데 하나는 한 버킷당 들어갈 수 있는 엔 트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 것입니다.
해당 버킷에 데이터가 이미 있다면 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현(연결리 트)하기 때문에 체인이라고 합니다.

해시테이블의 시간복잡도
"해시테이블의 탐색, 삽입, 삭제의 시간복잡도는 평균적으로 O(1)을 갖지만 충돌이 빈번하게 일어나면 최악의 경우인 O(n)의 시간복잡도로 수렴할 수 있습니다."
충돌해결(개방번지화 : Open Addressing)
open addressing은 chaining과 달리 한 버킷당 들어갈 수 있는 엔트리가 하나뿐인 해시테이 블입니다.
해시함수로 얻은 주소가 아닌, 다른 주소에 데이터를 저장할 수 있도록 허용한다는 취지에서 open addressing이라고 합니다.
해시충돌이 빈번히 생길 수 있습니다.

1) 선형탐사(Linear probing)
최초 해시값에 해당하는 버킷에 다른 데이터가 저장돼 있으면 해당 해시값에서 고정 폭(예컨대 1칸)을
옮겨 다음 해시값에 해당하는 버킷에 액세스(삽입, 삭제, 탐색)합니다. 여기에 데이터가 있으면 고정폭 으로 또 옮겨 액세스합니다.
2) 제곱탐사(Quadratic probing)
최초 해시값에 해당하는 버킷에 다른 데이터가 저장돼 있으면 해당 해시값에서 그 폭이 제곱수로 늘어
난다는 특징이 있습니다. 예컨대 임의의 키값에 해당하는 데이터에 액세스할 때 충돌이 일어나면 1**2칸 을 옮깁니다.
여기에서도 충돌이 일어나면 이번엔 2**2칸, 그 다음엔 2**3칸 옮기는 식입니다.
3) 이중해싱(Double hashing)
탐사할 해시값의 규칙성을 없애버려서 clustering을 방지하는 기법입니다.
2개의 해시함수를 준비해서 하나는 최초의 해시값을 얻을 때, 또 다른 하나는 해시충돌이 일어났을 때 탐사 이동폭을 얻기 위해 사용합니다.
for x in nH.values(): # O(N)
for x in nH: # O(N)
if x in nH.values(): # O(N)
if x in nH: # O(1)
for key,val in dic.items(): # O(N)
for key in dic.keys(): # O(N)
과 for val in dic.values(): # O(N)
'코딩테스트[파이썬] > 입문자를 위한 코딩테스트 핵심' 카테고리의 다른 글
| [해시] -빈도수2 [Counter] (0) | 2024.01.22 |
|---|---|
| [해시] -빈수도1 (0) | 2024.01.22 |
| [배열과 연결리스트와 덱] -두수의 합- (0) | 2024.01.22 |
| [배열과 연결리스트와 덱] - 중복제거- (0) | 2024.01.22 |
| [배열과 연결리스트와덱] -수열의회전 (0) | 2024.01.22 |